勾配・発散・回転の体積積分
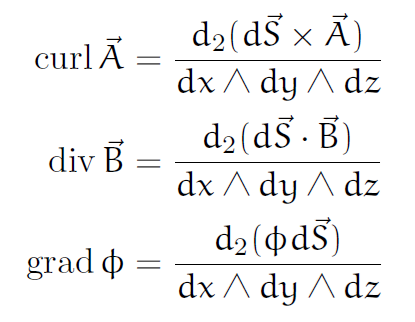
勾配・発散・回転の体積積分
勾配・発散・回転の体積積分が与えられることがある. これに関連した計算をDenker記法および外微分を用いて代数的に議論することができる.
なお以下は 濫用表記のすゝめ (微分記号) の補足ノートからの引用である.
回転の体積積分
$\vec{A}=(A_x,A_y,A_z)$ の回転 $\mathrm{rot}\vec{A}$ はDenker記法を用いて次のように整理できる.
\[\mathrm{rot}\vec{A} = \frac{1}{dx\wedge dy\wedge dz} \begin{bmatrix} dS_y\wedge dA_z - dS_z\wedge dA_y \\ dS_z\wedge dA_x - dS_x\wedge dA_z \\ dS_x\wedge dA_y - dS_y\wedge dA_x \end{bmatrix}\]ここで次を定義した.
\[d\vec{S} = \begin{bmatrix} dS_x \\ dS_y \\ dS_z \end{bmatrix} := \begin{bmatrix} dy\wedge dz \\ dz\wedge dx \\ dx\wedge dy \end{bmatrix}\]さてこの $d\vec{S}$ は $2$ 形式であるから,$2$ 形式への外微分 $d_2$ を用いて次のような整理ができる.
\[d_2(A_zdS_y) = dA_z\wedge dS_y = (-)^2dS_y\wedge dA_z = dS_y\wedge dA_z\]よって次のように $\mathrm{rot}\vec{A}$ を整理できる.
\[\mathrm{rot}\vec{A} = \frac{1}{dx\wedge dy\wedge dz} \begin{bmatrix} d_2(A_zdS_y - A_ydS_z) \\ d_2(A_xdS_z - A_zdS_x) \\ d_2(A_ydS_x - A_xdS_y) \end{bmatrix}\]ここで $d_2$ を各成分にかかるものとしても表記し,クロス積を用いれば,次のようにも整理できる.
\[\mathrm{rot}\vec{A} = \frac{d_2(d\vec{S}\times\vec{A})}{dx\wedge dy\wedge dz}\]これより体積積分および発散定理を用いることで,次の等式を直ちに得ることもできる.
\[\int_V \mathrm{rot}\vec{A} (dx\wedge dy\wedge dz) = \int_V d_2(d\vec{S}\times\vec{A}) = \oint_{\partial V} d\vec{S}\times\vec{A}\]発散の体積積分
同様に発散 $\mathrm{div}\vec{B}$ はDenker記法の下で次のように表記できる.
\[\mathrm{div}\vec{B} = \frac{d_2(d\vec{S}\cdot \vec{B})}{dx\wedge dy\wedge dz}\]これから発散定理を用いて,次の等式を直ちに得ることもできる.
\[\int_V \mathrm{div}\vec{B}(dx\wedge dy\wedge dz) = \int_V d_2(d\vec{S}\cdot \vec{B}) = \oint_{\partial V}d\vec{S}\cdot \vec{B}\]勾配の体積積分
最後に勾配 $\mathrm{grad}\phi$ はDenker記法の下で次のように表記できる.
\[\mathrm{grad}\phi = \frac{d_2(\phi d\vec{S})}{dx\wedge dy\wedge dz}\]よって次の等式が直ちに得られる.
\[\int_V \mathrm{grad}\phi(dx\wedge dy\wedge dz) = \int_V d_2(\phi d\vec{S}) = \oint_{\partial V}\phi d\vec{S}\]関連
Grassmann 代数と一階偏導関数 (Denker 記法)